Mathe Basics für die Mittelstufe (Klasse 7–10)
Übungsaufgaben Mittelstufe: Terme, Gleichungen, Funktionen & Geometrie
Fit fürs Abi in Mathe – Lücken füllen – Wiederholen – Üben
Welche Themen deckt das Buch ab?
- Terme und Rechenregeln
- Gleichungen und Ungleichungen
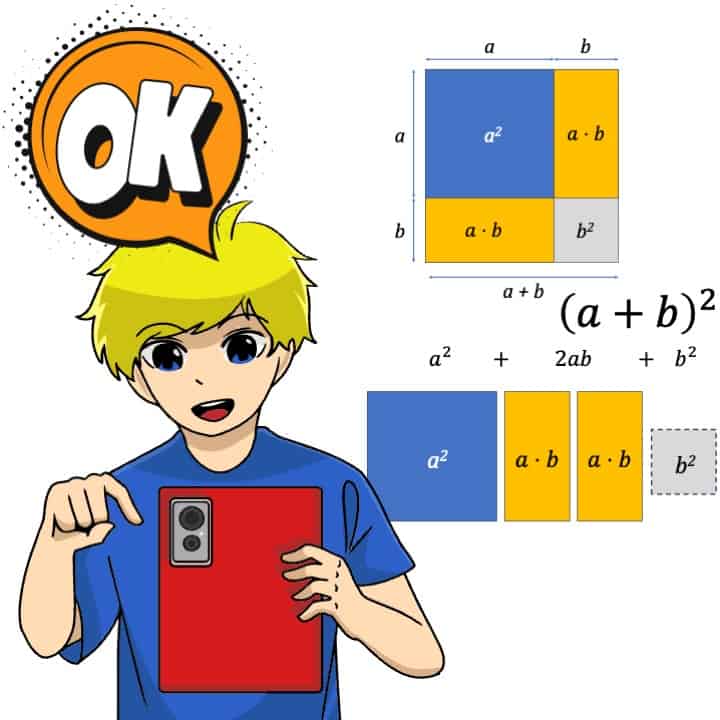
- Binomische Formeln
- Wurzeln
- Satz des Pythagoras
- Lineare und quadratische Funktionen, quadratische Gleichungen
- Geometrie und Körper
- Trigonometrische Grundlagen
Das komplette Inhaltsverzeichnis könnt ihr hier downloaden!
Warum Mathe Grundlagen üben?
Nutzen für Klasse 7–10 & Abitur
Das Buch „Die Mathe Basics aus der Mittelstufe“ als Übungsbuch wurde konzipiert, um den Stoff aus Klasse 6/7 bis 9/10 (je nach Lehrplan und Schulform) zu üben und zu wiederholen. Dabei liegt der Schwerpunkt auf Standard Aufgaben, die du auf jeden Fall können solltest. Die Themen wurden auch unter dem Gesichtspunkt der guten Vorbereitung fürs Abitur erstellt. Du kannst auch dabei einzelne Kapitel je nach Bedarf auswählen, um genau dieses Thema zu trainieren. Zu allen Aufgaben des Übungsbuch findest du die Lösungen auf über 130 Seiten.
NEU dabei:
Übungsbuch mit Lösungen + (demnächst) interaktive Aufgaben-Generatoren für unendlich viele Aufgaben zusammen erhältlich.
Ich werde hier auf mathefritz.com zu allen Aufgabentypen Aufgaben Generatoren für interaktive Matheaufgaben erstellen. Ziel des Buchs und der interaktiven Matheaufgaben ist es, mathematische Grundlagen der Mittelstufe sicher zu beherrschen. Das ist die Basis aus der Mittelstufe, für die Klassen 7, 8, 9 und 10, je nach Schulform. Übe die Mathe Grundlagen, um fit für das Abitur zu sein.
Der eine oder andere wird jetzt sagen, dass komplexere Aufgaben oder Textaufgaben zu den einzelnen Themen fehlen. Das ist an dieser Stelle aber auch nicht beabsichtigt.
Weitere fehlenden Themen werden wir in der 2. Jahreshälfte 2026 einarbeiten. Hierzu werden dann gehören: Wahrscheinlichkeitsrechnung, Geometrie und Winkelgesetze.

Seite 45: Übersicht Binomische Formeln und 1. Binomische Formel anschaulich erklärt.

Seite 65: Rechnen mit Wurzeln Hinführung mit einem typischen Beispiel
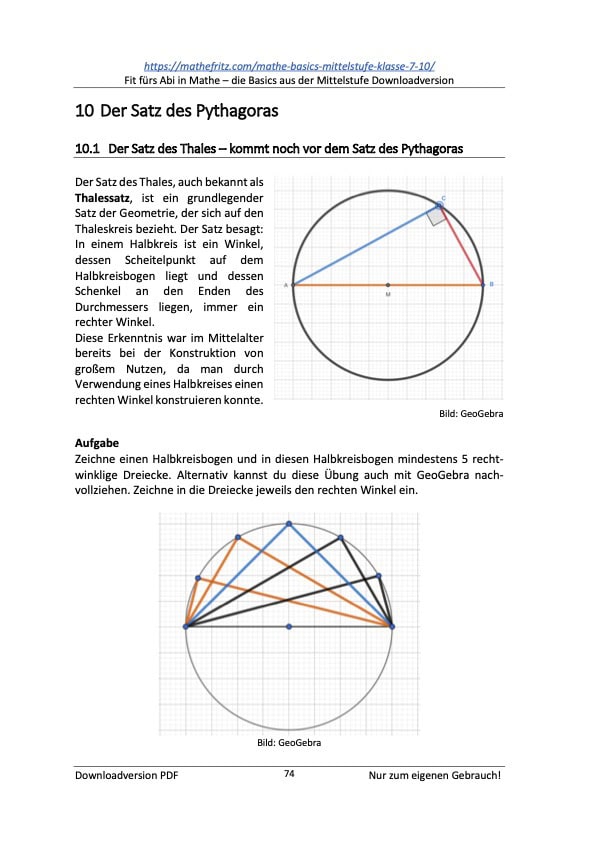
Seite 74: Satz des Pythagoras, ein elementares Thema in Mathematik in der Mittelstufe
Für wen ist das Mathe-Basics-Buch geeignet?
Fit fürs Abi, die Basics aus der Mittelstufe
Das Buch „Mathe Basics für die Mittelstufe” wurde entwickelt, um die bisherigen Aufgabenblätter der Mathefritz-CD zu ersetzen. Diese stammen aus den Jahren 2005 bis 2012, seit dieser Zeit haben sich jedoch alle Lehrpläne stark verändert. Ebenso haben sich die Aufgabenkultur und das Anforderungsniveau der verschiedenen Schulformen verändert. Darüber hinaus ist es sehr aufwändig, einzelne Aufgabenblätter auszudrucken. Viele von euch haben keinen Drucker mehr, sondern nutzen Tablets.
Schüler/innen der Klasse 7 – 10
- Schülerinnen und Schüler können sich je nach Unterrichtsinhalt das passende Thema heraussuchen und mit Aufgaben aus dem Buch eigenständig die Mathe Grundlagen üben.
- Besonders gut geeignet ist das Buch ebenfalls, um Lücken zu schließen. Wenn du feststellst, dass ein bestimmtes Thema als Basis für ein neues Thema beötigt wird, kannst du hier gezielt wiederholen. Z.B. beim Thema „Pythagoras“ musst du gut mit Wurzeln rechnen können.
- Bist du kurz vor der Oberstufe? Dann wird es so langsam ernst. Kannst du qudratischen Gleichungen lösen? Kennst du dich im Lösen von Gleichungssystemen aus? Falls nicht, kannst du hier gezielt Themen aus zurückliegenden Jahren wiederholen!
Eltern
- Für Eltern ist es das ideale Übungsbuch mit Aufgaben und mit Lösungen zu fast jedem Thema von Klasse 7 bis 10. Schnell kann man einen Aufgabenblock zur Einübung der wichtigsten Grundlagen, wie z.B. der Termumformung oder das Lösen einfacher Gleichungen heraussuchen die Rechnungen der Kinder und mit den Lösungen im hinteren Teil des Buchs vergleichen.
- Nach und nach werden wir zu ALLEN Themen des Buchs auf dieser WEB-Seite interaktive Aufgaben Generatoren bereitstellen. Mit diesen kann man unendlich viele Aufgaben üben.
- Gerade die wiederholte Rechnung von sehr vielen Aufgaben führt zuer Festigung des Stoffes und bringt Sicherheit für den nächsten Test oder die nächste Klassenarbeit.
Lehrkräfte
- Für Lehrkräfte bietet es zusätzliche Standard Aufgaben zu den einzelnen Themen, wenn das eingeführte Lehrbuch keine weiteren Aufgaben mehr anbietet.
- Die Apps sind eine ideale Ergänzung zum Unterricht und können allen oder nur Schülerinnen und Schülern mit Förderbedarf auch auf Lernplattformen zur Verfügung gestellt werden.
- Die Aufgaben Generatoren liefern auf die Schnelle ein Arbeitsblatt für einen Hausaufgaben Test, wenn die Schülerinnen und Schüler mit dem Aufgaben Generator eigenständig geübt haben.
- Ebenso schnell kann mit den Generatoren ein PDF Arbeitsblatt erstellt werden, z.B. als Hausaufgabe.
Aus dem Vorwort des Buchs
Das Buch wendet sich einerseits an Schülerinnen und Schüler vor dem Einstieg indie Oberstufe, um die wichtigsten Mathe Grundlagen zu wiederholen, die in der Oberstufe vorausgesetzt werden. Ebenso an alle Schülerinnen und Schüler in den Stufen 7 bis 10, um jeweils das aktuelle Thema zu üben.
Die behandelten Themen erheben keinen Anspruch darauf, vollständig zu sein. Dem ein oder anderen wird ein Thema fehlen oder ein Bereich zu wenig behandelt zu sein. In diesem Buch liegt der Schwerpunkt auf Übungsaufgaben. Theoretische Grundlagen werden in der Regel nicht hergeleitet. Die wichtigsten Regeln und Gesetzmäßigkeiten werden jedoch zu Beginn jedes Kapitels vorgestellt.
Rein geometrische Themen wie Ähnlichkeit von Dreiecken, Winkelsätze oder Dreieckskonstruktionen werden nicht behandelt, da auf diese Themen in der Oberstufe selten Bezug genommen wird. Ebenso verzichten wir auf das Thema Wahrscheinlichkeitsrechnung, da man sich dieses Thema in der Regel in der Oberstufe auch noch neu erarbeiten kann.
Die Themen können je nach Schulform und Bundesland in verschiedenen Jahrgängen behandelt werden. Sie stellen jedoch eine essenzielle Auswahl für eine gute Vorbereitung auf die Oberstufe oder zum Wiederholen des Stoffs eines Schuljahres dar.
Das Thema „Polynomdivision“ wird aktuell noch nicht behandelt. Bei einer Erweiterung des Inhalts steht dieses Thema jedoch an erster Stelle.
Aufbau: Regeln, Beispiele, Übungsaufgaben und Lösungen
Nutze das Buch mit den kurzen Erklärungen und den Aufgabenpaketen mit verschiedenen Aufgabentypen und Schwierigkeiten und dazugehörigen Lösungen. Das reicht aus, um für eine Klassenarbeit oder Schulaufgabe zu üben, Lücken zu schließen oder zu wiederholen. Um endlos zu üben, Sicherheit zu gewinnen und auf ein TOP Level zu kommen sind die Aufgaben Generatoren gedacht!
Um Missverständnisse zu vermeiden!
Der Schwerpunkt liegt auf dem Üben von Aufgaben. Die Erklärungen sind nicht ausreichend, um den Stoff zum ersten Mal zu erarbeiten oder zu verinnerlichen!
Das Lernpaket:
Buch mit kurzer Einführung und kurzen Regeln, Aufgabenpakete im Umfang von 3 -10 Seiten je Thema. Dazu zusätzlich: die online Aufgaben Generatoren für endloses Üben mit direkter Aufgabenkontrolle.
Inhalte & Kapitel:
Mathe Basics Mittelstufe (Klasse 7–10)
1. Terme aufstellen und vereinfachen in Klasse 7 oder Klasse 8
Überblick über Terme
Ein Term ist ein Rechenausdruck. Er kann aus Zahlen, Rechenzeichen, Variablen und mathematischen Symbolen wie z.B. Klammern bestehen. Einige Beispiele für Terme:
- 2 \cdot x + 3
- 4a + 10b
- 12\cdot ( 20\cdot x + 3\cdot x^2)
Terme werden vereinfacht, zusammengefasst oder ausgerechnet. Sie enthalten grundsätzlich kein Gleichheitszeichen. Steht ein Gleichheitszeichen zwischen zwei Rechenausdrücken, dann handelt es sich um eine Gleichung.
Wichtig zu wissen:
- Gleiche Variablen dürfen zusammengefasst werden.
- Wir dürfen NIE verschiedene Variablen (wie z.B. a und b) zusammenfassen.
- Reine Zahlen dürfen nicht mit Variablen zusammengefasst werden!
- Multiplizieren wir gleiche Variablen miteinander, so können wir dies als Potenz schreiben.
- Bei der Multiplikation dürfen wir Faktoren vertauschen, so dass die Variable im Produkt rechts steht und wir die Zahlenfaktoren miteinander multiplizieren können.
Wozu braucht man Terme? Ein Beispiel:
Wir betrachten das Gewicht eines Briefes in Abhängigkeit der Anzahl der Blätter in dem Briefumschlag einschließlich der Briefmarke.
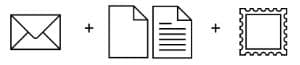
Wir nennen das Gewicht des Briefumschlags u , das Gewicht eines Blattes Papier p und die Anzahl der Blätter Papier nennen wir n . Das Gewicht der Briefmarke nennen wir b Dann lautet der Rechenausdruck für das Gesamtgewicht:
u + n\cdot p + b
Kennen wir die einzelnen Gewichte in Gramm und nur die Anzahl der Blätter Papier ist unbekannt, können wir den Rechenausdruck auch schreiben als:
7 + n\cdot 5 + 3
In diesem Term wiegt der Umschlag 7 Gramm, ein Blatt Papier 5 Gramm und eine Briefmarke 3 Gramm.
Unseren Term kann man zusammenfassen zu:
10 + n\cdot 5
Darf ein Standardbrief maximal 20 Gramm wiegen, wird schnell klar, dass n maximal 2 werden darf, d.h. man darf nur zwei Blätter in den Briefumschlag einlegen.
2. Gleichungen lösen – linear, mit Klammern, mit Brüchen
Warum muss man Gleichungen lösen können?
Das Lösen von Gleichungen ist elementar wichtig in der Mathematik. Wir benötigen diese Technik in vielen späteren Themen als Hilfsmittel zum Lösen anderer Problemstellungen. Zwei wichtige werden hier einmal vorgestellt:
1. Bestimmen der Nullstellen von Funktionen
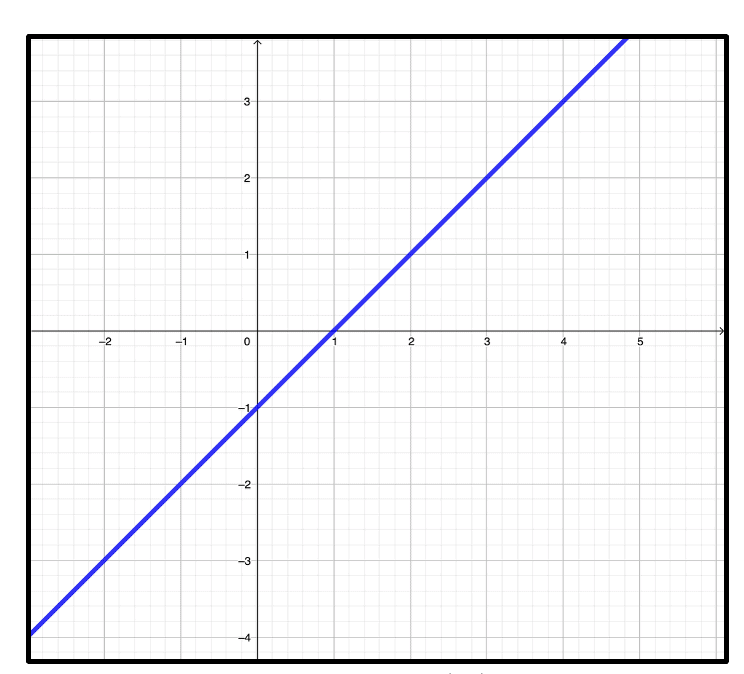
Bild: GeoGebra, f(x)=x-1
Wo hat die Funktion:
f(x)=x-1
eine Nullstelle? Die Gleichung, die wir lösen müssen, lautet:
x-1=0
Forme um und du erhältst ganz schnell die Lösung:
x=1
2. Gleichsetzen von Funktionen, Schnittpunkt finden
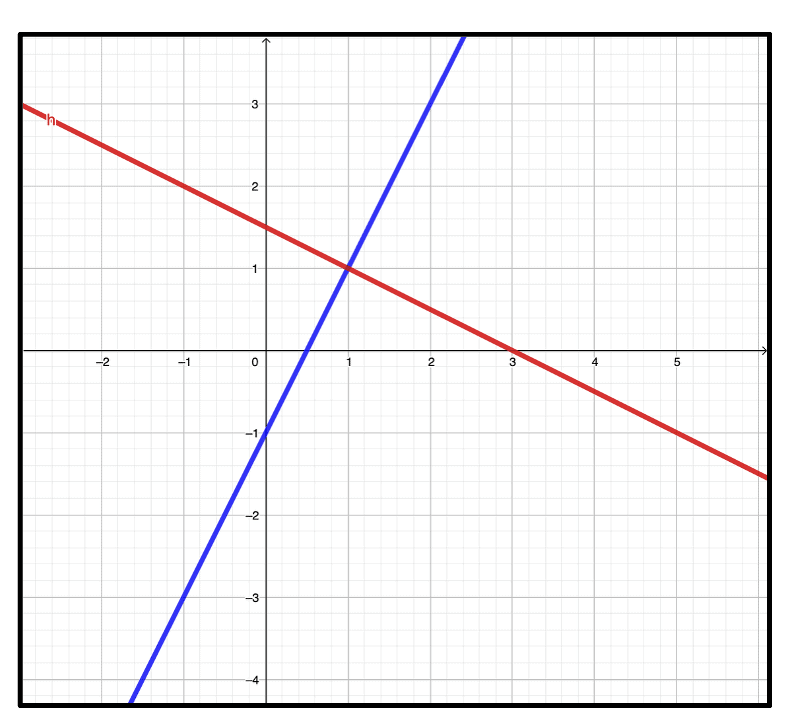
Bild: GeoGebra,
f(x)=2x-1, g(x)=-0,5x+1,5
Wo scheiden sich die Funktionen:
f(x)=2x-1, g(x)=-0,5x+1,5
Setze beide Funktionsterme gleich. Die Gleichung lautet:
2x-1=-0,5x+1,5
Aufgelöst nach x erhalten wir: 2,5x = 2,5
Oder ganz aufgelöst: x=1
Viele weitere Erklärungen und Übungsaufgaben zu dem Thema Gleicungen in meinem Buch! Die Aufgaben Generatoren für unendliche viele Aufgabenblätter folgen in Kürze!
3. Ungleichungen lösen – Regeln & Beispiele – Klasse 7 und Klasse 8
Besonderheiten beim Lösen von Ungleichungen:
Ungleichungen löst man prinzipiell wie Gleichungen, mit einem wichtigen Unterschied:
Multiplizieren oder dividieren wir Ungleichungen mit oder einer anderen negativen Zahl, so dreht sich das Ungleichzeichen um! Beispiel:
-x>2 |+x
\Leftrightarrow 0>2+x | -2
\Leftrightarrow -2>x |
\Leftrightarrow x<-2
Oder direkt mit der Regel:
-x>2 | \cdot (-1) und Ungleichzeichen umdrehen!
x<2
Als Lösungsmenge geben wir bei Ungleichungen immer ein Intervall an, in unserem Beispiel:
L=]-\infty ; 2[
Kennst du dich mit der Intervallschreibweise aus? Übe auf 3 Seiten mit Aufgaben wie man Ungleichungen löst und die Lösung als Intervall angibt, oder demnächst zu diesem Thema mit dem Aufgaben Generator Ungleichungen!
4. Lineare Funktionen – Steigung, Achsenabschnitt, Graph – Klasse 8
folgt bald!
5. Lineare Gleichungssysteme – Additionsverfahren, Einsetzungsverfahren, Gleichsetzungsverfahren
folgt bald!
6. Binomische Formeln – 1.-3. Formel und Binomische Formeln rückwärts
folgt bald!
7. Quadratische Terme faktorisieren – mit Beispielen und Übungen
folgt bald!
8. Bruchterme vereinfachen – Rechnen mit Brüchen in Termen
folgt bald!
9. Wurzeln berechnen – Wurzelterme und Wurzelregeln in Klasse 8 oder Klasse 9
folgt bald!
10. Der Satz des Pythagoras – Anwendungen, Dreieck, Klasse 9
folgt bald!
11. Potenzen mit ganzzahligen Exponenten – Potenzgesetze – Klasse 9
folgt bald!
12. Parabeln und quadratische Funktionen – Anwendungsbeispiele – Klasse 9 und Klasse 10
folgt bald!
13. Quadratische Gleichungen lösen – pq-Formel & quadratische Ergänzung Steigung
Klasse 9 und Klasse 10
folgt bald!
14. Trigonometrie – Sinus, Cosinus und Tangens – praktische Anwendungen
folgt bald!
15. Der Kreis – Formeln, Kreiszahl Pi, praktische Beispiele
folgt bald!
Didaktik
Einsatz in Unterricht, Nachhilfe und Fördermaßnahmen
Passende Apps zum Buch:
Über uns – wer steckt hinter Mathefritz?
Mathefritz ist eine Lernseite für Mathematik und Informatik des Mathe-, Physik- und Informatik- Lehrers Jörg Christmann.
Meine Erfahrung:
Seit über 20 Jahren unterrichte ich Mathematik, Physik und Informatik. Mein besonderer Schwerpunkt liegt in der einfachen und verständlichen Erklärung von komplexen Themen. Und seit kurzem auch in der Erstellung von interaktiven Apps und Übungsblättern zum online lernen. Probiere es aus, viel Spass dabei wünscht dir Jörg!
Unsere bisherigen Seiten https://mathestunde.com und https://mathefritz.de werden wir mittelfristig durch diese Seite ablösen!