Bruchrechnen Aufgaben
Meistere Bruchrechnen spielend mit den besten Übungen

Mit Mathefritz lernst du die
Bruchrechnung schnell und interaktiv!
Bruchrechnen Aufgaben richtig verstehen
Lerne Brüche leicht und effektiv zu meistern! Unsere Bruchrechnen Aufgaben sind genau das Richtige für dich. Brüche können auf den ersten Blick einschüchternd wirken, aber mit den richtigen Tricks und Übungen kannst du das mühelos beherrschen.
Unsere Auswahl an Bruchrechnen Übungen ist darauf ausgerichtet, dir das Verständnis von Brüchen zu erleichtern und dein Selbstvertrauen im Umgang mit Brüchen zu stärken. Von grundlegenden Bruchoperationen, der Addition und Subtraktion von Bruchteilen bis hin zur Multiplikation und Division in komplexeren Aufgaben bieten unsere Übungen eine umfassende Abdeckung aller relevanten Konzepte.
Egal, ob du Schwierigkeiten mit dem Addieren, Subtrahieren, Multiplizieren oder Dividieren von Brüchen hast, unsere Übungen werden dir helfen, deine Fähigkeiten zu verbessern. Dabei bieten wir dir interaktive online Aufgaben mit direkter Kontrolle der Lösungen wie auch die klassischen Bruchrechnen Aufgaben als PDF zum Ausdrucken, natürlich mit Lösungen.

Bruchteile berechnen –
der Einstieg in die Bruchrechnung
In diesem Kapitel lernen wir zunächst einmal Bruchteile kennen. Wie nennt man die Teile eines Bruchteils? Was von einem Bruchteil ist der Zähler und was ist der Nenner? Hierzu finden wir viele Bruchrechnen Aufgaben interaktiv oder als Bruchrechnen Übung mit Lösungen als PDF zum Ausdrucken!
Die Bruchrechnen Aufgaben:
Kürzen und Erweitern
Kürzen und Erweitern von Brüchen sind grundlegende mathematische Operationen, die auf Bruchzahlen angewendet werden, um sie in verschiedene Formen zu bringen, ohne ihren Wert zu ändern. Diese Konzepte sind besonders wichtig, wenn man Bruchrechnen Aufgaben mit algebraischen Ausdrücken rechnet.
Das Kürzen eines Bruches beinhaltet das Teilen von Zähler und Nenner durch einen gemeinsamen Teiler, um den Bruch in seiner kleinsten Form darzustellen. Ein gemeinsamer Teiler ist eine Zahl, die sowohl den Zähler als auch den Nenner ohne Rest teilt. Durch das Kürzen wird der Bruch einfacher und übersichtlicher.
Um einen Bruch zu erweitern, multipliziert man sowohl Zähler als auch Nenner mit demselben Faktor. Dieser Faktor kann eine ganze Zahl oder sogar ein Ausdruck sein. Die Erweiterung ermöglicht es, den Bruch in eine äquivalente Form zu bringen, die den gleichen Wert hat, aber möglicherweise eine andere Darstellung aufweist.
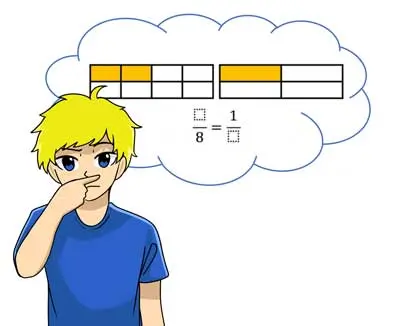
Lust auf eine erste kleine Übung, oder direkt zu unserer Seite zu den Brechnrechnen Aufgaben Kürzen und Erweitern!
Dezimalbrüche lernen
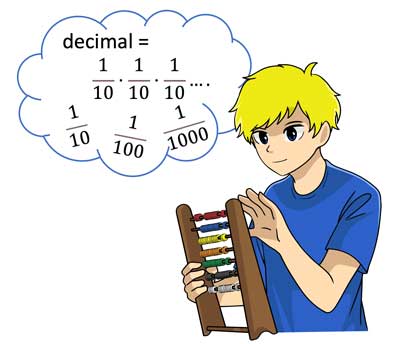
Kannst du Bruchrechnen Aufagebn mit Dezimalzahlen? Diese nennt man auch Dezimalbrüche. Brüche kann man immer in Dezimalbrüche umwandeln, wenn man die Zähler in eine Zehnerpotenz oder auch Zehnerzahl durch Kürzen oder Erweitern des Bruchteils umwandeln kann. Hier nur ein kleines Beispiel.
Bruchrechnen Aufgaben:
Prozente und Brüche

Brüche kann man als Prozentwerte darstellen und umgekehrt. Weißt du wie das geht? Hierzu muss immer im Nenner des Bruchs 100 stehen. Dazu muss man den Bruchteil erweitern oder kürzen. Weißt du, was zwei Fünftel als Prozentwert sind?
Genau, es sind 4 Zehntel oder 40 Hundertstel und damit 40%.
Prüfe dein Wissen. Wie gut kannst du Bruchrechnen Übungen mit Prozentwerten? Probier es hier schon einmal aus.
Bruchrechnen Übungen: Brüche addieren und subtrahieren
Um Brüche zu addieren, müssen sie denselben Nenner haben. Falls sie unterschiedliche Nenner haben, muss man sie zuerst auf den kleinsten gemeinsamen Nenner (dazu braucht man das kleinste gemeinsame Vielfache) bringen.
Nachdem die Brüche denselben Nenner haben, addiert man einfach die Zähler und behält den gemeinsamen Nenner bei. Das Ergebnis ist ein neuer Bruch. Beispiel:

Schon Lust auf eine erste Bruchrechnen Aufgabe, bevor es zum großen Lernpaket Addition und Subtraktion von Brüchen geht?
