Задачі на обчислення дробів
Вивчайте дроби з легкістю з найкращими вправами

З Mathefritz ви можете вивчати дроби швидко та інтерактивно!
Правильне розуміння дробів
Навчіться легко та ефективно вправлятися з дробами! Наші вправи з математики дробів саме для вас. Дроби можуть здаватися страшними на перший погляд, але за допомогою правильних прийомів та вправ ви опануєте їх без особливих зусиль.
Наша добірка вправ з математики дробів створена, щоб допомогти вам зрозуміти дроби та розвинути впевненість у роботі з ними. Від базових операцій з дробами, додавання та віднімання дробів до множення та ділення в більш складних завданнях – наші вправи охоплюють всі необхідні поняття.
Якщо у вас виникають труднощі з додаванням, відніманням, множенням або діленням дробів, наші вправи допоможуть вам покращити свої навички. Ми пропонуємо вам інтерактивні онлайн вправи з прямим контролем рішень, а також класичні вправи з дробами у форматі PDF, які ви можете роздрукувати, звісно, з рішеннями.

Обчислення дробів – Початок роботи з дробами
У цьому розділі ми вперше дізнаємося про дроби. Як називаються частини дробу? Що таке чисельник і що таке знаменник дробу? Ми можемо знайти багато інтерактивних задач з математики дробів або вправ з математики дробів з рішеннями у форматі PDF, які можна роздрукувати!
Задачі на обчислення дробів: скорочення та збільшення
Скорочення та розширення дробів – це основні математичні операції, які застосовуються до дробів для перетворення їх у різні форми без зміни їх значення. Ці поняття особливо важливі під час обчислення дробів за допомогою алгебраїчних виразів.
Скорочення дробу передбачає ділення чисельника і знаменника на спільний дільник, щоб представити дріб у найменшій формі. Спільний дільник – це число, яке ділить чисельник і знаменник без остачі. Скорочення робить дріб простішим і зрозумілішим.
Щоб піднести дріб до степеня, помножте чисельник і знаменник на один і той самий множник. Цей множник може бути цілим числом або навіть виразом. Піднесення до степеня дає змогу перетворити дріб в еквівалентну форму, яка має те саме значення, але, можливо, інше представлення.
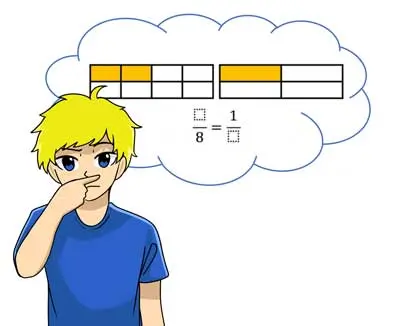
Хочете виконати першу невеличку вправу або перейти безпосередньо на нашу сторінку із завданнями Brechnrechnen Скорочуй і розширюй!
Вивчення десяткових дробів
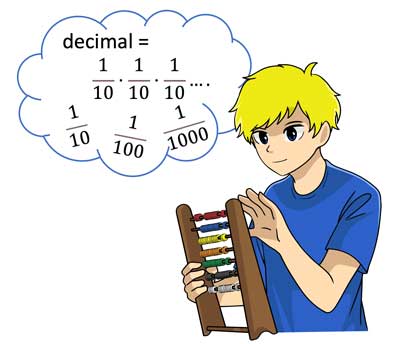
Чи вмієте ви обчислювати дроби з десятковими дробами? Такі дроби ще називають десятковими. Дроби завжди можна перетворити на десяткові, якщо ви можете піднести чисельник до десяткового степеня або до числа десятків, зменшивши або збільшивши дріб. Ось лише невеликий приклад.
Задачі на обчислення дробів: Відсотки та дроби

Дроби можуть бути представлені у вигляді відсотків і навпаки. Чи вмієте ви це робити? Знаменник дробу завжди повинен дорівнювати 100. Для цього потрібно розширити або скоротити дріб. Чи знаєш ти, що таке дві п’яті у відсотках?
Саме так, це 4 десятих або 40 сотих, а отже 40%.
Перевірте свої знання. Наскільки добре ви виконуєте вправи з дробами та відсотками? Спробуйте тут.
Вправи з дробами: Додавання та віднімання дробів
Щоб додати дроби, вони повинні мати однаковий знаменник. Якщо вони мають різні знаменники, їх потрібно спочатку звести до найменшого спільного знаменника (для цього потрібно знайти найменше спільне кратне).
Оскільки дроби мають однаковий знаменник, ви просто додаєте чисельники і зберігаєте спільний знаменник. В результаті ви отримаєте новий дріб. Приклад:

Хочете виконати першу задачу на обчислення дробів, перш ніж перейти до великого навчального пакету з додавання та віднімання дробів?
